��ѧ��ģ�ĵ����
���������Ƕ������������������µ�˼��ʱ��ͨ���Ϳ���дһƪ�ĵ���Ὣ��������������ܹ�����Ŭ����ǰ�Ķ������������ôд�ĵ��������������С��Ϊ�����������ѧ��ģ�ĵ���ᣬ����Ҳο������ϣ��������������Ҫ�����ѡ�
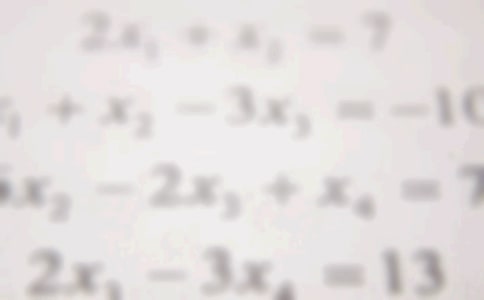
��ѧ��ģ�ĵ����1
�����ڳ��������ѧϰ�����У����ǽӴ��������Ŀ��������ѧһֱ������ѧϰ���ص㡣����ѧ��ģ����ѧ������ѧ�е�һ����֮�ǡ�ͨ��ѧϰ��ѧ��ģ�����Dz����������ѧ˼ά�������������˴�����ʶ���ŶӺ�����������ƪ�����У��ҽ���������ѧϰ��ѧ��ģ�����е������ĵá�
�������ȣ�ѧϰ��ѧ��ģ��Ҫ���Ǿ߱���ʵ����ѧ��������ѧ��ģ�漰��������ѧ֪ʶ��������������Ρ�����ͳ�Ƶȵȡ��ڽ�������У����Dz�����Ҫ��֪��Щ֪ʶ��ĸ����ԭ��������Ҫ�ܹ���������������õ�ʵ�������С���ˣ���ѧϰ��ѧ��ģ֮ǰ����������Ҫ�����ѧ����������Ҫ�������ո���֪ʶ�㣬��Ҫ�ܹ���������֮�����ϵ��Ӧ�á�
������Σ���ѧ��ģҪ�����Ǿ߱����õ���˼ά�������ڽ��ʵ������Ĺ����У�������Ҫ���������������ϵ��Ȼ����������Ҫ����н�ģ�����ó�����ʵ������Ľ����˼ά������������Ҫ����ƽʱ�����˼�������������������Ҫ�������ù��ɡ��������ȵȷ�����ͨ�����ϵ���ϰ��˼�������ǵ���˼ά������õ���Ч�Ķ�������ߡ�
����Ȼ����ѧ��ģ��Ҫ�������ŶӺ����ľ����ڽ��ʵ�������'ʱ������ͨ����Ҫ��ͬѧ��һ��������ۺ��о�����ͬ��ɽ�ģ�����ŶӺ����������Լ�˼���棬�����ǻۣ������Զ������ǵĹ�ͨ�����ͺ�����ʶ����ˣ���ѧϰ��ѧ��ģ�Ĺ����У�����Ҫѧ����������ϣ��������˵Ĺ۵㣬�����ֹ�����ͬŬ����ɹ�ͬ��Ŀ�ꡣ
�������⣬��ѧ��ģ��Ҫ���Ǿ߱�������ʶ���ڽ��ʵ������Ĺ����У����Dz���Ҫ�������еĽ��ⷽ��������Ҫ���ô��µ�˼ά��ʽ�ͷ�����������⡣���ǿ���ͨ����ͬѧ�ǵ����ۺ��о�����������ʦ��ר����̣�Ѱ���µĽ���˼·�ͷ�����ͬʱ�����ǻ����Բο����е��о��ɹ���ʵ�����飬�������õ��Լ��Ľ�ģ�����У����������Լ��Ĵ���������
���������ѧ��ģ�̸����ǵIJ���������ѧ֪ʶ�ͼ��ܣ�����һ��ѧϰ̬�Ⱥ�˼ά��ʽ��ѧϰ��ѧ��ģ�����ǴӴ�ͳ������Ӳ���н��ѳ��������������ǵ���ѧ�����ͽ���������������ѧϰ��ѧ��ģ�Ĺ����У�������Ҫ���ԣ�����̽������������������ս��ֻ�в��ϵ�˼����ʵ�������Dz��ܸ������������ѧ��ģ�ı��ʺ�������
����ͨ��ѧϰ��ѧ��ģ��������ظ��ܵ���ѧ��������ʵ���ԡ���ѧ��ģ����һ�ſ�ѧ������һ��˼ά��ʽ�ͽ������Ĺ��ߡ��ڽ���ѧϰ�������У��ҽ�����Ŭ��ѧϰ��ѧ����֪ʶ�����������Լ�����ѧ��ģ����������ѧ����������������ʵ�����⡣
��ѧ��ģ�ĵ����2
������ĿǰΪֹ�������Ѿ�ѧϰ��ѧ��������ѧ��ģ���ſγ̰��ѧ���ˣ������Ķ����ſγ��е��˽��ˡ��Ҿ��ÿ�����ѧ��ģ��һ��ѧ����Ӧ��ʱ���ķ�չҪ����Ϊ�����ſ�ѧ�����ķ�չ���ر��Ǽ���������ķ��ٷ�չ�㷺Ӧ�ã���ѧ�о��빤�̼�����ʵ��������о����Ͼ�ȷ���������������ֻ���ʹ����ѧ�ڸ�ѧ�ơ������������������ǿ������ѧ��ģ����һ�����е�������Ϊͻ������ǰһ�ε�ѧϰ�����˽���������Dzμ���ѧ��ģ������ѧ����Ҫѧ�ģ�Ҳ�������Ǵ������Ե��о�ѧϰ�����ſγ�����ʵ�������������кܴ��Ӧ�ã�ͻ������ǰ��Ҷ���ѧ����⣬Ҳ��һ���̶�������������Ӧ����ѧ���߽��ʵ�������������
���������Ͻ̲�����˵���ںܶ�ʱ��α����.��������ʵ��������������ӣ��������Ǹ��ܹ�����ʵʵ���ܵ����ſγ̶�ʵ����������İ����������������ǿ�����ѧ���ſ���ʲô���ð�����ֱ���˷�ʱ�䰡ʲô�ġ�
���������Ҿ�˵˵�ҵ�ĿǰΪֹѧ����ʲô�����ȣ���֪������ѧ��ģ�Ļ������裺��һ�����ǿ϶���Ҫ����ʵ�������Ϣ���ɱ���Ϊ���ǵ���ѧģ�ͣ�Ȼ������ǽ�������ѧģ�ͽ�����⣬��һ��Ҳ����˵����ѧģ�͵Ľ�����һ������Ҫ��Ҫ���Ǹ���ѧ����ع鵽��ʵ���磬Ҳ���ǽ���ѧģ�͵Ľ��ת��Ϊ����ʵ����Ľ�𣬴Ӷ���һ������֤��ʵ�������Ϣ����һ���Ƿdz���Ҫ��һ�����ڣ���Щ���Ҳ��Ҫ��ʵ�ʵ���Ϣ������֤��
�������������һ���̶��Ͻ�ʾ����ʵ�������ѧ��ģ�Ĺ�ϵ��һ���棬��ѧ��ģ�ǽ���ʵ�����е�������Թ��ɡ�����IJ����Դ����ʵ��ȴ�ָ�����ʵ����һ���棬ֻ�е���ѧģ�͵Ľ������ס��ʵ����ļ���ʱ���ſ�������ָ��ʵ�������ʵ���������ٻع鵽ʵ������һѭ����
�����ڿα��ڶ��µ�ʱ�����ǿ�ʼ�Ӵ�ʵ�����⣬�ڵڶ���Ƭͷ���ǿ����ľ���ij���й�ˮ����Ԥ�����⣬����һ�����ʦͨ�����й�ˮ����Ԥ������������������Ʊ���ʽ�IJ�ֵ������Ϸ������й�ˮ��Ԥ��ļ�������ˮ�������ʹ�����ֵ��,���в�ֵ����Ҫ����Lagrange����Newton�����ֶεʹβ�ֵ������������ֵ���������Dz������������ѧ��ģ��ʵ�������İ�����
������ͬʱ������Ҳ���֣�Ҫѧ����ѧ��ģ��һ��ѧ�ƣ�����˵Ӧ����ѧ��ģ��֪ʶȥ����������⣬������ֻҪ����������ʵ����ѧ֪ʶ������Ҫ����ѧϰ�������ѧ��֧ѧ�ƣ�������ʱ�����ǻ���Ҫ��������ѧ�����������ǽ�����⣬ͬʱ��Ҫ����ʵ�����ѧ���ʵ��������������ѧ���⡣
�����ܵ���˵��ѧϰ��ѧ��ģ��һ��ѧ�ƶ����ǵİ����ܴ���Ϊ��������ǿ���ҵ�֪ʶ�棬���ǿ�����ѧϰ��һ��ѧ�ƵĹ����ж�������ѧϰ�����ԣ���������ǿ����ѧ�����ͷ����������������������������ʦ�����Ժ����Ͻ���������λҲ�Ǻ��а����ġ�
��ѧ��ģ�ĵ����3
����������xx�켶ר������ѧ������ǰ����ר�Ƶ�ʱ������ѧϵ�����βμӹ���ѧ��ģר���龺����ȥ����·ݣ�������ר����ѧ������ѧϵ�������������ϵ��һ��ѧ�ڣ��Һ������ܴ��������ϵȥ�μ�2004��ĸ߽̱�ȫ����ѧ����ѧ��ģ������ľ�����
�������Ƕӹ���������Ա�������ϡ��������Ͳ̺�����ָ����ʦ����������ʦ����˵�����ˣ����е��ź���ֻȡ��ʡ���Ķ��Ƚ������ܽ�����ҽ�����ѡ������ԭ�����Ǵ��л����dz�������˲��ٵľ���ͽ�ѵ��
����ͬ���Dzμӹ���ר����ľ�����ȣ��˴εľ����������Ƕ��ԴӸ����涼����һ��̨�ס�
���������DZ�������֯���棬ͬר��ʱ����ǰ����ȣ����DZ��ξ�������ǰ�������˶�ʮ��ĸ�ǿ�ȷ��ʽѵ�������⣬��������һ�αȽ������ģ�⾺������ͬѧ���������������ĵ�״̬��ѧУ���ڴ˴α���Ҳ�DZȽ����ӵģ������ṩ�˱ȽϺõ�ѵ���������ϻ�������ʹ��ҿ�����һ�����ۣ���̸���飬�ֿ�ͨ�������Ѽ�������ϣ�����ÿ��������ɵ���ʦ�����ǽ��и�����������ʣ�ʹ���ǵ�ѵ����Ч����������һ��̨�ף�Ϊ����ȡ�úóɼ����»�����
������Σ���ģ�͵��ѶȺͶ���Ƶ�Ҫ�ǵ�������ר������ɵ���Ŀ��һ���ǡ�������������̰��š�����һ���ǡ����ɳ����������ǻ��������г�ʶ��Ӧ�������⣬�������漰��Լ�������Ż����⣬�Ѷ�һ�㲻�Ǻܴ����ߵĴ�Ҳ�������ܽӽ�����ȷ���ȵ��Dz�����˭��ģ���Ż��ø�������������������ʵ�á�����ͨ�����ڿ�ʼ������ĵ�������������ģ�͵Ľ�����д���ı��ij��壬ʣ��ʱ��������ڴ���ģ�͵�һЩϸ��������ı��ĸĽ����⣬ʱ����ԱȽϳ�ԣ��ȥ��������ɵ���Ŀ�ǡ����˻���ʱ������������Ż�ģ�͡����漰�����ģ��Ӧ��ģ�͵���ƺ��Ż����⣬�ѶȽϴ��漰ѧʶ�ķ�ΧҲ������ֻ����ѧ�ͼ����������������ڶ���ۺ���֪ʶ����ʹ������Ľ�ģʱ�䣬Ҳ�ܷ���ģ����������Ľ��ĵط�����ʱ���϶�����ñȽϸϣ����ڴ˴ξ����������ڽ���ģ�ͺ�д�ı��Ϸ����ʱ�䲻�����������ͽ�ģ�����˼���ȫ����'ʱ�䣬�ı��ı�д�����Ʒ�����Եò���ô�淶��
��������Ǹ�����������ߡ�ͨ���μ���ģ�����������ߵ������������ʹ���˼ά�����õ����������������õ����Ե���ߣ��������������е�̬�Ⱥͼ�ֲ�и�ľ������ǽ��һ������Ĺؼ����������ŶӺ��������ʵ�ɵľ����������Ա֮����ϵýϺã������ķֹ�Э�������ཻ����ȡ�����̣���ʵ����ȥѰ��������ķ�����
�����ܸ�лѧУ�ṩ������һ����ô����IJ������ᣬ�˴εľ��������Ƕ�Ա��ָ����ʦ����ʦ���Ѿ��������������Ҫ����Ҫ�����������ڴ˴ξ������ܽᾭ��ͽ�ѵ��Ϊ��һ�ξ���������������ʵ�Ļ�����ϣ���������´ε���ѧ��ģ��������ȡ�úõijɼ���
��ѧ��ģ�ĵ����4
�������ȼ�Ҫ�Ľ���һ���ҵ��������ѧ��ģ��Ҳ���ڴ�һ��ٿ�ʼ�Ӵ��ģ�֮ǰ����û���κε��˽⡣�ұ�������ѧҲ����ԽϺ����Ȥ��ͬʱ��Ҳ�Ǽ����רҵ��ѧ������ˣ��Ҿ����ҿɲμ���ѧ��ģ�������������һ����ٲμ��˹���������˹�һ������ĺ��ٲμ����������ɼ���δ֪��
������������˵˵���ڱ���ǰ��ĸ��ܡ�����ǰ������ѧ��ģȱ���㹻���˽⣬ֻ֪����ѧ��ģ��Ϊ3�����֣���ģ����̣����ġ�ͬʱ����Ҳ�μ���Ϊ��һ���µ���ѵ�����ڱ��˵�ʱ�����ţ�����ǰ�漸�����迨�ǣ����ջ���ѡ����������һ���֡���Ҳ�ʹֵ�ͬѧһ����Ϊ���������Ҫ�ģ�ֻҪģ�ͺã�����㷨�þ��С����ǣ��������Ǹ�����ʦ�����ң�������һ����������ȡʤ�ġ�ģ�����㷨��ֻ�ǻ����ģ���û��ʲô���ʵĵط���
������ˣ��ܵ���˵���ڱ���֮ǰ����Ҫ���ϵͳ�Եı�����ѵ���ر��Ƕ��㷨�����ա��㷨�ǽ������ĺ���Ҫ��һ���֡����Ƽ������Լ�����Ҫ����ʦ�����ǽ�һ�½���Դ��ʦ�ġ�ģ�����㷨����һ���飬�Ȿ������ѧ��ģ�ľ����鱾����ѵ���������μӱ�����ͬѧ���Բ�ͬ����ȥ���գ�����ÿ����������һ�ž�ͨ��һ�����գ�һ���˽⡣����ѵ�����ѧ��ģ���������һ�����˽⣬�ڴ��˽�֮�Ͽ��Կ�ʼ��ʽ����Ŀд�����ˡ�
�������Dzμӹ������������ѡǰ�����������Ŀ����Ϊ��Щ��Ŀ�����������ĵģ����Բο���Щ�������ģ�ѧϰ�������ĵ�д���ַ���ѧϰ������������д��ģ�ͺͳ�����Щ��Ŀ���ʺ����ż���ͬѧ���ġ��������ڱ���ǰ�ܹ�����7�������Ŀ���Ҷ�����������ģ�
������Щ��Ҫ���������ֵģ�ǰ��ƪֻҪ��ȥѧϰ���˵�д����������ģ��ʽ�ͱ�̷����������漸ƪ���Ǹ���ѧϰ����д���ģ��������ܲο����˵����ġ�д���Լ������ĺ�����һ���Լ��ı������ϡ�����ڱ���ǰ2�죬����Ҫ��ȥ����Ŀ�ˣ��ͺú÷���һ�£��ú�˯˯������ǰΪ��������������˵������ɣ����Կ���֮ǰ���������ϡ�
�������ڽ�ģ��ͬѧ��Ҫ���ն����㷨������˵������Ҫ��Щ���ԣ�����������1��2���㷨���ܹ���ϸ�Ľ��͵ġ����ڱ�̵�ͬѧ�����˵�Ǽ����רҵ�ģ���ô��MATLAB��Ҫ��Ϥ���ã���Ϊ��ģ��ͬѧ��ɺ���Ҫ��̵�ͬѧ���ܽ��������д���ĵ�ͬѧ�����Ը����Լ��ľ����ڱ���ǰ��������ĵ�ģ�塣���������ڱ���ǰд������ģ�塣
���������У������ǵ�һ�βμӱ������ر��ر�Ľ��š�һ�õ���Ŀ��ȫ���ĵ�Ͷ�뵽�����У��ֻ�Ҳ�������κ��ţ�QQ����Ϣ�����������Լ���ʱҲ�ر�ķ��������һ��ʼ��A�������Ȥ��������һ������Ҳ���۲���������Ȼ����������ѡ��B�⣬��������ѡ���ʱ�仨�ѻ������ر�Ķ࣬���������ǽ�ģ����̺�д���ġ��Լ�������ĵIJ����ģ������ġ�
�����������ҵ�ʱͻȻ���ò��ܵ������û�л��Լ������ٹ��Ļ���ͦ��ʵ�ģ������ҷܶ�����Ŭ����������˵��û���������ڼ����������������ֻ������ǣ���Ȼ���˹�һ��ȷʵ�����ҵ����ϡ�����Ϊ�������ӵ�����è�����ܹ���һ��ʡһҲ�е�̧�����ˣ��ܳ�����������Ҳȥ�μ����人�İ佱��ͻȻ��ʶ�����Լ��IJ��㣬��һ�Ķ���Ҳ�������������Һܶ���鶼�����˱�����Ա������ܽ���Ľ�����һ����ȱ����ʶ��
�������ڷֹ����ҽ�������ͬѧÿ���˷ֱ���һ�Ȼ��ģ��ͬѧ��Ҫ�����ĵ�д���������գ���̵�ͬѧ��Ҫ�Խ�ģ�������գ�д���ĵ�ͬѧ��ȫ�ֶ�Ҫ��һ�����ա��������������ĵ�ͬѧΪ�����ġ�
���������Ǵ��ҵĽǶȣ������дһƪ��ʽ������������`����дһЩ���⡣�������ĵ��Ű��������£�
��������Ŀ�����ڹ�����������Ҫд�������滯һ�㣬���磺
����1�����ڶ�Ŀ��·���滮���Ż�����
����2�����������̹滮ģ�͵���ֽƬƴ�Ӹ�ԭ�����о�
������ժҪ����һ�����Ƕ�ȫ�ĵ��ܽᣬ������ƪ���¶�д�����ɡ�Ҫ�������Լ����࣬��Ҫ�ж���ķϻ������Խ���Ҫ�Ĵ�����б��
��������������Ϊ����дժҪʱ���Ȳ�������Ҫ��������ʲô��Ȼ��д�����Dz���ʲôģ�Ͷ��������⡣��������ϸ��������Ŀ�������̡����д����������������
�����۹ؼ��ʣ���һ����д���µ���Ҫ����Ŀ�꣬������õ��㷨��Լ4��5����
����ժҪ�ؼ���Ҫ�������һҳ���ڣ����ܳ���һҳ
������������������Ϊ���ⱳ���������������������������Ŀ���Լ����Խ���������ʱ���������ٸ�����Ŀ��
����������������Բ�ͬ������ֿ�����
�������У���Ҫд�������Ҫ������������ģ�ͣ��Լ���ϸ���������������̣�����Ϊ��ժҪ����ϸ�档
������ģ�͵ļ��裺����������Ŀ�Ĺ����л�������裬д���ĵ�ͬѧ��Ҫ��������Ŀ��ʱ��ǵ�д���������������ǡ�
�����߷���˵�����������ľ����ÿ����������ĵ���ʦ�������õ�ӡ��
��������˵����ò�Ҫ�ֿ���ҳ��д���������˴������ĸо���������ҳ���ÿ���
������ģ�͵Ľ�������⣺������������ģ�ͷֵ����ۡ�
����������һ������Ϊ����������дģ�͵����Լ����ݵ�Ԥ������Ȼ��д��ģ�͵Ľ�������һ���ֶ���������ģ����ϸ�IJ�������������дģ�͵���⣬���дģ�͵Ľ���ͷ�����
�����������ȷ��������Ʊ������������ı������������ȵķ���
������ģ�͵��������ƹ㣺ģ�͵�����д����������ģ�͵��ŵ���ȱ�㡣ģ�͵��ƹ�д��������������ģ�Ͷ�����������߶�δ����ʲô���á�
��ѧ��ģ�ĵ����5
������Сѧ��ѧ��ѧ��������ѧ��ģ˼�룬һ��Ҫ���պ���ѧ��ģ���ں�������ֻ���Ͷ����ˡ��ڽ�ģ�������ע����ѭСѧ���Ķ�ͯ�ԡ���֪ˮƽ�Լ�˼ά�ص㡣ͨ������������龳�ý�ģ˼������ȥ����Сѧ������ʵ����̽�����������γ�һ�ֽ�ģ���ܣ�������ģ��˼ά���������ý�ģ�ļ�ֵ����Ҫ�ԣ�������λСѧ��ѧ��ģ��
������ѧ��һ���о�������ϵ���ռ���ʽ�Ŀ�ѧ����Ҫ�ص��Ǹ���ij����ԡ����������ԡ����۵���ȷ�ԡ���ϵ�������ԡ�Ӧ�õĹ㷺�ԡ��������о���ѧ����ѧϰ��ѧ����Ŀ���ǽ���ѧӦ��������������ᡣʵ�ִ�Ŀ�ĵ�;���ǰ�ʵ����������ѧ��ϵ������ͨ����ѧģ����ʵ�ֵġ���ģ�ͻ�����ѧ�е�һ������������������е���ѧӦ��֮���ࡱ��������ѧģ������ѧѧϰ����Ҫ���֡���ѧ��ģ�������λ�����ã����ѴӴ�ѧ������������졣Сѧ��չ����ѧ��ģ�Ƿ���У��ճ���Сѧ��ѧ��ѧ��᳹��ģ˼���Сѧ��ѧ��ѧ����ʲô�����һ��ֵ��������⡣
������ѧ��ģ�ĺ��ı���������ͻ�����ֶ�ԭʼ����ķ��������衢����ͻ��������ѧ��ѧ���ߺͽ�ѧ�����Լ���ѧģ�͵�ȡ�ᡢ�����ӹ����̡���ѧģ�͵ķ����D�D���D�D��֤�D�D�ٷ����D�D�ĨD�D����D�D�����ĵ������̸������ر��ֳ�ѧ��ѧϰ��ѧ��Ӧ����ѧ���ʵ������Ĺ�ϵ������һ�������Ĺ��̣����ֳ�һ�֡��͵Ŀ��й��̡���ʹѧ����Ŀһ�¡��ⲻ���ٽ�ѧ������ѧ��ʶ�ļ�ǿ����ѧ��������ߣ�����Ҫ���Ǵٽ�ѧ������ѧƷ�ʵ������������Ǹ�У���dz���Сѧ����ѧ��ģ�ļ�ֵ��ѧ����ѧϰ�������������Ӱ�죬��������ѧ��ѧ��Ҫ�᳹��ѧ��ģ˼�룬�ؼ���������β��ܰ��պ���ѧ��ģ���ں�����β���չ��һ���������̣���ο�ѧ��λ����һ����Ҫ��˼�����⡣�������ѧ��ģ��ʵ�塢Ŀ�ꡢԭ��;����һЩ���ۡ�
����һ����ģ����Ķ�ͯ��
�����ڳ���ѧУ��ѧ��ģ��������Сѧ����֪ʶ���õ��ص���Сѧ��ѧ�������Сѧչ����ѧ��ģ�����������龳��һ��ע�����ո����Ե��ʶȣ�������ѧ���������չ��������Ҫ�ԡ����ü��������š�Ϊԭ��ֱ��ѧ���ġ����ŷ�չ������Ҫ������λ��ѧ��ģ���Ѷȡ���ȡ��¶ȡ��ʶȣ�����Ҫѧ������˼��������̽������Ҫѧ������̽���������⣬����������ѧ֪ʶ������⡣
����1���ڽ�ģ���������顣��ѧ��ģ�ṩһ����������ʵ�������龳������ʵ����������ѧ�йص��زļ�ʱ���뵽ѧϰ�����У��ѽ̲����ݽ������ʵ�ʡ�����ȵ㡢��Ȼ����������ѧ�����й�ϵ�ĸ������أ������ת��Ϊ��ͯ�ճ�������ѧ����Ļ���˼�������䵱����������֧������������ѧ��ʹѧ������ѧϰ��Ȥ����ѧ�������߾�����龳�з������⡢������⡢������⣻��ѧ����ʶ������ļ�ֵ�ԣ���ѧ��ץס�����ê����ʧʱ���ļ���ѧ����̽����Ȥ������飬��ʹѧ���û��۵ľ�����������龳����������ѧ���⣬ʹѧ�����콫��������������ѧ���⣬��֪��ѧģ�͵Ĵ��ڡ�
����2���ڽ�ģ�������֪ˮƽ����������ʵʩ��ѧ��ģ��Ҫ���ʩ�̣�ѭ�����ܼ�������������Ҫ�ʺ�ѧ����������������Ҫ����һ������ս�ԣ���������ѧϰ��ѧ����Ȥ���������ѭ������ѧ������֪���ɺ���֪ˮƽ����������׳̶�Ҫ���У��ٴ����ʺ�ѧ����չ�IJ��죬����ѧ���ĸ��ԣ�ͬʱ���ѧ����ʵ��һ��Ҫ�ֲ�����ƽ�ʵʩ������ǰ�����ѧ��ģ��ѧ������֪����С�˼ά�ȵ��ص㡣�������������ڶ�ͯ���������룬�������ڵ���ѧ��������̽���Ļ����ԣ��������������ǵĽ�ȡ��������ʶ��
����3���ڽ�ģ����˼ά�ص㡣������Сѧ��ѧ��ѧ������У���ʦӦ��ȡ��֮��Ч�IJ��ԣ���ǿ��ѧ��ģ˼���������ѧ��ͨ����ģ�γ�һ�ּ��ܣ��γ�һ����ѧ��˼ά��������������Щ��ѧ��˼ά�������������⡢������⣬��������ǵ�'����Ŀ�ġ��磺Сѧ��ѧ��ƽ��������ʶ����һ����ƽ������Сѧ����˵�dz����֪ʶ��������������֪ʶ�����ھ���������龳�С���ʦҪ���þ���������龳����ѧ����ν������н�����������ݣ�����˼ά��ͻ���Ӷ��ƽ���ѧ˼����������У����ִӾ���������龳�г��ƽ������һ��ѧ����Ĺ��̣�����һ�ν�ģ�Ĺ��̣�Ҳ��ѧ����ƽ�������������֪�Ĺ��̡���Сѧ��ѧ��ѧ�У����ʺ�ѧ��ˮƽ����ѧ��ģ�����뷽�������ÿ��ø�Ϊ�鶯��Ϊ���ʵĻ��
����������ģĿ���ָ����
������Сѧ�����Σ�����ѧ��ģ����ѧһ����������ѧǰ�صĸ��˲ź���ѧ��ģ�����μ����������Ǵ���Ϊ������������νӽ��е���ѧ��ģ����ѵ��������Ϊ������Сѧ������ѧ����ΪĿ�ġ���Сѧ�������������Ծ��ġ����������ġ����е�������ѧ��ģ˼�룬������⡢�������⡢������⡣��Ϊ��ʦ��Ҫ����ѧ������ѧ������������ϣ��ҵ�������֪ʶ�����ϵ㣬������Ϊ���������ѧ������ģ�ͣ���ѧ�����齨ģ���̲����γɽ�ģ˼�롣
����1������ѧ����ģ��ʶ����Сѧ��ѧ��ѧ�н�ʦҪͨ��������ʵ�����ѧ��Ϊ�����龳��̽�������⣬��ѧ����ȷ����Ӧ����ѧ�����Щʵ�����⡣��ѧ��������뽨ģ�Ĵ�����̣��Ӷ������Щʵ�����⣬������ѧ��ʵ��Ӧ����������Ṧ�ܡ���ʦҪվ�����ѧ��˼ά���������̬�����ֵ�۵ȷ��������ѧ��ģ����ʶ��Ϊ��Ҫ�����һ�Ҫע������ѧ����ѧ���Ե�ת����������ѧ�Ķ�����������
���������֮�����Ǵӽ̵ĽǶȽ�����ѧ��ģ��������ѧ��������ѧģ�͡��γ���ѧ˼��Ĺ��̡����Ǵ�ѧ�ĽǶȽ�����������̽�������ֽ������Ծ�Ӧ�õĹ��̡�Ȼ���᳹��ģ˼���Сѧ��ѧ��ѧ������ע������ѧ��ѧ����ȴ��������ѧ��ģ�ĺˡ�������ʦȱ����ѧ��ģ��˼����ʶ����ȱ��ָ����ѧ��ģ�IJ��ԣ���ģ֮·���������
����2��ѧ�����齨ģ���̡���ѧ��ģ����Ҫ����ʵ������ʵ�������������������Ϊ��ѧģ�ͣ��ڸ�����ѧ���ɽ���������⣬��֤ģ�͵ĺ����ԣ����ø���ѧģ�����ṩ�Ľ�������͡�Ӧ����ʵ����Ĺ��̡�վ��Сѧ���ĽǶȣ���ѧ��ģ������ѧ���������齨ģ�Ĺ��̣�ͨ��ʵ�������龳����ѧ���ڽ�ģ�����и�����ѧ�γɺʹ���Ĺ��̡�������Ϊ��ѧ��ģ̽���Ĺ���������Ҫ�Ļ��ڣ�Ҫ������Сѧ��Ӧ����ѧ��˼����ʶ�᳹��ʵ�����������У�����۲졢�������ۺϡ���������������������ģ�ͣ������ѧ���⣬���ʵ��������������̡�
����3��ѧ���γɽ�ģ˼�롣ʹѧ���������յ���ѧ֪ʶ����������й۲졢�������������ܽ�����ʵ���⣬ʹѧ����������ܹ�������������ı��ʣ����Ծ�������ת����ѧģ�ͣ�������������ѧģ�ͣ�������Ϣ����������������裬���г�������������ض���������ϵ���������֪ʶ������⡣ͨ����ѧ��ģ���γ���ѧ��ģ˼�룬��ѧ��������ᵽ���ļ�ֵ���ڣ������˽���ѧ֪ʶ�ķ������̣���ǿѧ��ѧϰ��ѧ����Ȥ����߷������⡢������������������֪����ѧģ�͵Ľ������������յģ�Сѧ���γ�ģ����ʶ������˼ά���������������ʵ�����⣬�ٽ����ҵ���ѧ������������ѧ����˼����Ǹ�����Ŀ�ġ�
����������ģ˼�������
����Сѧ��ѧ��ѧһ��Ҫ������ѧ��ģ�ĺˣ���Ҫ�ý�ģ��Ϊ��ʽ�Ĺ�������ѧ������Ҫ����ʶ�ش���ʵ�ʵ������龳���ý�ģ˼������ȥ����Сѧ������ʵ����̽�����������γ�һ�ֽ�ģ���ܣ�������ģ��˼ά��������ѧ����ѧ����ѧ֪ʶ��ϵͳ�������������ܽ��ʵ�����⡣���ǻ�����ͨ��������ʽ����ѧ���������⽨ģ�Ĺ��̺���Ҫ�ԣ���ѧ��ѧ���ڴ�����ѧϰ��
����1��ѧ��ģ�ڽ̲���ѡȡ����ʦ����Ҫ�ӽ�ģ�ĽǶȶԽ̲Ľ��н����Сѧ��ѧ�̲��У����������Ѿ����գ��������龳�D�D����ģ�ͨD�Dģ����֤�D�Dģ�ͽ�����Ӧ�á���ģ��˼·�����˱��š���ʦҪ����ھ�̲����̺��Ľ�ģ˼�룬��Ҫ����û�ơ�����ѡ�������ѧ���ݵ�ʵ�����⣬����ѧ����ѧ֪ʶ���ļ�������ѧ��������ģ�ͽ����ʵ���⡣��Σ��ڽ�ѧ��������ʺ��ý�ģ˼��չ����ѧ�����ݡ���ʦ����ѧ��ģ˼�����̲����ݣ����������еĽ̲����ݶ��ʺ���ѧ��ģ��Ҫ���ʺ���ѧ��ģ�Ľ̲ĺ�ϵͳ������������������������ѧ��ģ������ȷ�����ý�ģ˼��չ����ѧ��ѧ��
����2��ѧ��ģ�ڿ��������졣��ѧ��ģ�Ŀ��ý�ѧ�Ǹ��������龳�ԡ�̽���ԡ���չ�ԵĽ�ѧ�����ص��Ƕ�ѧ����ѧ��ģ�����Ŀ�����˼ά�ļ�����˼���Ѭ�ա�ѧ���ۺ�ʵ������Ǵ�ͨѧ�ƽ��ޣ��ٽ�ѧ�����ͨ��Ψһ;��������Сѧ�����̲İ��ŵ�̽����ʵ���ǣ�
������һ������ʵ����������涨�ߺ涨����ļ���ͼ�Σ�ѡ��Сľ�����������塢���������ܣ�������ֽ���ò�ͬ��������Բ������бȽϡ����㡢���֡�̽����
�����ڶ��������������D�D�����ճ����������üҾߡ��ҵ��װ�ijߴ粢�����ܳ�����������������Բ�����������ݻ��������ʾ�ߴ����Ƚϣ�Ѱ�������аٷ�����Ӧ�õȡ�
������������չʵ��Ӧ��һ�D�D���ռ�������ʹ�÷��������ݹ�ʽ�����ͥ�����ϵ�������ݹ�ʽ����ͬѧ���ѵı����غͽ���״����
�������ģ���ѧ���ɷ��֨D�D̽�����ɡ�����ƽ����֮�����Ϊ�ߣ����Ի���������������Ҫ������״����������Ρ���ʦ����ѧ������Ƚϣ���ѧ���������ֿ��ŵļ�ֵ���ڣ���Ҫ������ѧ֪ʶ���Ӧ�õĹ�Ч�������ξ���Բ��������ѧ��ƽ��ˣ����ľٶ�������Ҫ��������������ͬ�벻ͬ��������������Ǩ�Ƶ������У����磺ͬ���IJ���Χ������������ʹ�ݻ����ȡ�
�������̲���ijЩ���˽�ģ��������������ݽ��к������ϣ���ȷָʾ��ģ�����⣬�ؿ�ѧ������ѧ֪ʶ������ѧ����˼·��ѵ��ѧ��˼ά������Ӧ����ѧ֪ʶ�����ʵ���⣬���ѧ������ѧ�������ۺ���������Ͻ̲ľ������ݣ������̾ߡ�ѧ�߲�������ԵĽ���ʵ�ʲ�����������磺���������֪ʶ��ѧ������������ӡ������ı����ף����ñ�����֪ʶ����ѧ���˽⽨����ĸ߶ȵȵȡ�
����3����ѧ��ģ��ʵ������չ��Ŀǰ��ͬ�汾�Ľ̲ģ������ˡ�ʵ�����ۺ����á��롰��֪����?�������Ľ�ѧ���ݣ�����������ʵ������ϣ���ѧ�����н�ģָ�������ڽ̲����ݵ���Ҫ���Ѹ�֪ʶ��������ϣ��������������龳����������ġ���ģ���⡱����ʵ��������⡣�磺Сѧ��ѧ�̲��С������ͼ�����̡�����������չ��Ϊ���ҡ����ҵȷ���װ���ṩ��ѧ���۵����̷�������չ�����Ľ�ģ��չ����ܼ���ѧ���ķ�Ӧ���������ҿ�������������һ�ִ����Ե�ѧϰ��������������ѧ��ѧϰ��ѧ��Ӧ����ѧ�ʹ�����������������ǡ���ģ֮�ϵĽ�ģ����
��ѧ��ģ�ĵ����6
����д��ǰ�棺
������ѧ��ģ��һ���ִ�����ѧ�Ʒ�������һ�ֽ���ѧ��ʵ��Ӧ�����ϵķ�������һ��ͨ��������ѧģ��������������ʵ�����Ⲣ������Ӧ�Ľ�������ķ�������ѧ��ģ�ѽ�����Ϊ����ѧ����һ�ֲ���ȱ�ٵ��ֶκ�һ�ֱ����˼ά��ʽ�������ڽ�����ѧ��ģ�Ĺ�������һЩ�ĵ���ᣬԸ���������ҡ�
����һ����ģǰ
�����ڽ�����ѧ��ģ֮ǰ��һ��Ҫ���˽���Ҫ��������⡣����ָ���˽���ָ����������һ�����µ���ʶ�����⣬֪������ľ���֢�������֪�����������������һ���ı���֪ʶ��ֻ�г���˽����⣬���ܸ��õĹ滮��ģ�ķ�����ص㡣
�������磬��������Ҫ���һ������վ̨�ϵ����������⣬����Ҫ�˽�ľ����������վ̨�ĵ���λ�á��ܱ������������Ű�����ȵȣ����ܸ��õ��ƶ������������
����������ģ����
������ģ���̿��Է�Ϊ�ĸ����裺���ⶨ�塢ģ�ͼ��衢ģ�ͽ�����ģ����⡣
�������������ⶨ�壬������Ҫͨ��ǰ����˽⣬������������Ҫ��������⣬��ȷ�����Ŀ�ĺ���Ҫ�õ��Ľ����
���������ģ�ͼ��裬����Ҫ�������ⶨ�壬����һЩ���裬�ƶ������ǵ���ⷽ��������ģ�ͽ��о�ϸ����ơ�
����Ȼ����ģ�ͽ�����������Ҫ����ǰ�������ļ��衢�滮����������Ч����ѧģ�͡�
���������ģ����⣬������Ҫ�������ǽ�������ѧģ�ͣ����м��㡢�������ó�һ�����ŵĽ����������������֤���Ż���
����������ģ����
����������ѧģ�͵ķ����кܶ࣬����������ѧͳ�Ʒ����������������Ż����������淽���ȵȡ��ڽ�����ѧ��ģʱ��������Ҫ������������Ժ�����Ŀ��.��ѡ����ʵķ������������ۺ�Ӧ�ã����ܵõ���Ϊȷ�����õĽ��������
�������磬ij��˾��Ҫ���������ƻ��ľ��ߣ����ǿ��������Ż�������ͨ��������ʷ���ݺ��������������������Ż���ѧģ�ͣ������������Ž⣬�ó����Ż��������ƻ����ߡ�
�����ġ���ģ����
����������ѧģ�Ͳ�����һ�ξͿ��Եõ��������Ľ�������л��漰�����ݲ�ȷ����ģƫ������⡣�ڽ�ģ�Ĺ����У�������Ҫ���е����������Ż���ֱ���õ�һ������Ĵ𰸡������д����һ������Ҫ���в��ϵIJ��Ժ��Ŵ���
�����塢�ܽ��뷴˼
������ģ�Ĺ��̲������Եõ��������Ĵ𰸣�����Ҫ���Ƕ��������ǵ�˼ά�����ͽ����������������ǿ�����������ģ�����ж��Լ��ı��ֺͷ��������ܽ��뷴˼���Ӳ������ҵ������ķ����������Լ��Ľ�ģ������֪ʶ��ϵ��ֻ��ͨ�����ϵ��ܽ�ͷ�˼�����ܸ��õ�����ѧ��ģ�з����Լ��IJ��Ǻ�������
������֮����ѧ��ģ��һ���ܹ�ʹ������Ч���ʵ�����⡢������ǵ��ۺ������ʹ��������ķ�����ͬʱҲ��һ��ʹ���Dz�������Լ��ķ�����ϣ������ܹ��������������Լ�����������������أ�
��ѧ��ģ�ĵ����7
�������գ���У��չ��һϵ�н�����������Ҳμ�������һ�Σ��ջ��ķᡣͨ����ν���������������dz��������ʶ����֪ʶ����Ҫ�ԡ����棬�ҽ��ʹ˴ν��������ݡ�����������ѧϰ���Եȷ�����н���������
�������ȣ���ν�����������ְҵ�滮���ڽ����У������˽��ʲô��ְҵ�滮�Լ�ΪʲôҪ����ְҵ�滮��ְҵ�滮��Ϊ�������Ǹ��õ�ѡ���Լ���ְҵ����ʹ�����ڽ����ľ�ҵ�и���˳����ͨ��ְҵ�滮�����ǿ��Գ�ַ����Լ������ƣ�����ʧ��Ŀ��ܣ�����Լ��ľ��������˴ν����У���ʦ�����������Ը����ǽ�����ְҵ�滮����Ҫ�ԣ������Ƕ�δ����ְҵ��·���˸���������ʶ��
������Σ��Ҵ���ν����еõ��˺ܶ������������ȣ���������ְҵ�滮���ܵȴ������л��ѧ�βſ�ʼ������Ҫ�����ڿ�ʼ��������Ǵ����˳�������ƽ�ʱ�ڣ��Ժ��ְҵѡ��Ϳ��ܻ��ܵ��ܴ��Ӱ�졣��Σ�Ҫ����ְҵ�滮������Ӧ���˽��Լ�����Ȥ���س�����ȷ�Լ������ƺ����ơ�ֻ���ҵ������ʺ��Լ���ְҵ�����ܸ��õط�չ��ͬʱ���һ�������ְҵ�滮����һ�ɲ���ģ�����Ҫ��������ԣ���ʱ�����Լ��ļƻ���
����ְҵ�滮��������һ�������Ե����⣬������Ҫ����ʵ���ġ��ڽ����У���ʦ�����ǽ�����һЩʵ�õķ����Ͳ��衣���ȣ����ǿ���ͨ�����˽ⲻְͬҵ�Ĺ������ʡ�н�ʴ�������չǰ���ȷ������Ϣ��Ϊ�Լ���ְҵѡ������������Σ����ǿ��Բ���һЩʵ�������ʵϰ��־Ը�߷���ȣ�ͨ��ʵ���������Լ���������Ϊ������ְҵ��·���������������Ҫע��˼���ͷ�˼����ʱ�����Լ���ְҵ�滮������ȷ�������Լ���'Ŀ����һ�¡�
����ͨ����ν������Ҷ��Լ���ѧϰ����Ҳ���˸������ʶ��Ľ������ȣ�����ʶ������������Լ���Ψһ;����ͨ���Ķ������鼮���ҿ����ؿ��Լ�����Ұ���˽�����֪ʶ����Ϣ����Σ���Ҫ���������Լ���ѧϰʱ�䣬�γ����õ�ѧϰϰ�ߡ�ֻ�б��ֹ��ɵ�ѧϰ����������Լ���Ч�ʡ����⣬�һ�Ҫע��ʵ����������ѧ����֪ʶӦ����ʵ����ȥ�������������Լ���֪ʶ�õ����á�
�����ܵ���˵����ν������Ҷ�ְҵ�滮���˸�������˽⣬�������Ҷ�δ�������顣��������ְҵ�滮����Ҫ�ԣ�ѧ��������ʵ�õķ����Ͳ��ԡ�ͨ����ν������һ������˶�֪ʶ�����ӣ���ʶ�����Լ���֪ʶ�ϵIJ��㡣�ҽ�����Ŭ��ѧϰ����������Լ���������Ϊ������ְҵ�滮��������
��ѧ��ģ�ĵ����8
��������������һ���ؼ���ʱ�ڣ�Ҳ��һ��ѧ�������зdz���Ҫ�ĽΣ�����������Σ�ѧ�����γ����Լ���ѧϰϰ�ߺ���Ϊ�淶��Ϊδ���ķ�չ�춨�˻�����Ϊ������ѧ�������õļ�����ʶ��������ǵ�����������ѧУ������֯��һ�����ɽ���������ν������������������������˺ܶ�������ᡣ
�������ȣ�����ʶ�����ɵ���Ҫ�ԡ������У���ʦͨ��������������������������������Υ�����ɵĺ���Ƕ�ô���ء���˵��һ�й�����ƶȶ���Ϊ��ά�������ƽ����Υ�����ɾ��Ƕ����������ƽ�IJ����ء�������˵�����һ��ѧ�������ٵ����ˣ�������Ӱ���Լ���ѧϰЧ���������������ͬѧ��ѧϰ��������ʦ�Ľ�ѧ���ȡ���Щ��������Ƕ��Լ������˵IJ������Σ�Ҳ�Ƕ�ѧУ�ͼ�ͥ�IJ����ء���ˣ�����Ӧ��ʱ�������Լ����ع����������õ���Ϊϰ�ߡ�
������Σ��������˼���Լ��������֮��Ĺ�ϵ����Щ����Ϊ���ؼ��ɻ������Լ������ɣ���ʵ���ϣ��ʵ��ļ����ƶȿ��Ա�֤���ǵ����ɵõ����õķ��ӡ�ͬ�������ɵ�����Ҳ������һ�ֻ��Һ��������У���ʦ��һ�������г��ı������������˽��ͣ�ֻ���ڼ��ؽ�ͨ�����ǰ���£����Dz���������ﳵ��ֻ������У��У�ͣ����Dz���������Ļ�����ѧϰ�ͳɳ���������һ�������Լ����������ʹ���������������ɣ�����������������ȷ�ļ�ֵ�ۺ���Ϊ��
�������⣬�һ���ᵽ���������θеĹ���������Ҫ���������ճ��������������棬���������ǰ���Ƕ��Լ������Ρ�������Dz������ؼ��ɣ����������Ͷ����Լ������θС������У���ʦ˵����û�м��ɣ���û�����Σ�û�����Σ��������Լ������˸��𡣡���仰������м��ɺ����θ�֮��Ľ�����ϵ��ֻ�����ؼ��ɣ�����ʱ�������Լ�Ҫ�������ģ������Լ�Ӧ���������飬���ܳ�Ϊһ���е������ˡ�
����������������ü��ɵļ�ֵԶԶ�����������塣���ɵ������������ܰ��������������õ���Ϊϰ�ߣ�����һ�ֵ��������ķ�ʽ�������̻ܽ������������ˡ����ع����������渺�����˺�г�ദ��һϵ����Ҫ�ĵ���Ʒ�ʡ����ܹ�Ӱ�����ǵ�˼�롢��к���Ϊ��ʹ���dz�ΪƷ�����㡢���ʹ�Ӳ���ˡ���Щ�����Ʒ��������һ������Ϊ����������Ѻ���սʱ��`����֧�֡�
������֮����μ��ɽ������������ʶ���˼��ɵ���Ҫ�ԣ�Ҳ���������˼���Լ��������֮��Ĺ�ϵ���Լ����������θ�֮��Ĺ�����ͬʱ����Ҳ��ʶ������ѵ����������һ����Ϊ�ϵ�Ҫ���Ƕ����������˸��������ͨ�����ؼ��ɣ��������������õ���Ϊϰ�ߣ���������ȷ�ļ�ֵ�ۺ���Ϊ��ͬʱҲ������Լ���������������Щ��Ϊ����δ���ijɳ��ͷ�չ�����˼�ʵ�Ļ�������ˣ�������������ؼ��ɵ���Ҫ�ԣ����������Ժ��ѧϰ��������ʱ�̱��ֺõļ�����ʶ��
��ѧ��ģ�ĵ����9
��������ѧ��ģ��һ����Ҫ�ϸ�������ѧ�ʣ���Ҫ�߱��ḻ����ѧ֪ʶ����˼ά����������ѧϰ�Ĺ����У��������ʶ������ѧ��ģ����Ҫ���Լ���ʵ�ʹ����������е�Ӧ�ü�ֵ���������ҵĶ���ѧ��ģ���ĵ���ᡣ
������Ϊһ��������ư������ѧ�����Һ���Ϳ�ʼ�˽Ӵ���ѧ��ģ������һ��ʼ��ʱ���Ҳ�û����������ʲô����ѧ��ģ��ֱ���ڴ�ѧ��ѡ����ϵͳ��ѧϰ��һ�š���ѧ��ģ��Ӧ�á��γ̺��ҲŶ���ѧ��ģ���˸��������֪�����⡣
��������ģ���ĺ�����˼�ǽ����ӵ�.ʵ������ת��Ϊ��ѧģ�ͣ�Ȼ������ѧ�������������Ⲣ������ѧ��������ʵ�ʵĹ����������У�����Ҫ��ԡ��о��������г�Ӫ�����������䡢������ͼ����Ƶ�Ȳ�ͬ��������ⶼ����ͨ������ģ���ķ�ʽ������⡣
������ѧ��ģ��Ҫ������ʵ����ѧ���ף�ͬʱҲҪ�ڱ�̼������������ԡ�������Ϊ��ѧ��ģ��������Ҫ���õ��ܶ����ݷ����ɸѡ�����ݿ��ӻ�������������ʵ�ֵȼ��ܡ�ֻ�н���ѧ�ͱ�̼���������ϣ�����Ϊ��ѧ��ģ�ṩ��������������
����������֪ʶ�Ļ����뼼������������֮�⣬��ѧ��ģ�л���Ҫ��עʵ�����⡣���Dz��ܽ����ۺͼ�����ʵ�����⻮�ֿ��������еġ���ģ��������Դ��ʵ�����⣬��ˣ��ڷ���ʵ������Ļ����ϣ����Dz��ܹ��и�������Ŀ�����ʵ��Ŀ���ѭ���IJ��衣
������ѧ��ģ��Ҫ�㷺ѧϰ�ͽ���������Ҫ�Ķ���������̽�ֺ����ģ���ȡ�������ҵ֪ʶ��ͬʱ�����ǻ�Ҫ�����μ�ѧ������ͽ������������ѧ�ߺ�ר��Эͬ���������̽�֣����������֪ʶ�������������Լ��Ľ�ģ������
�����ڶ���ѧ��ģ�Ĺ����У���Ҳ���������ྭ�䰸�����������ģ����̽����ѧ����ı��ʣ�����Ӧ����ѧ��DZ������ѧ��ģ��һ��ѧϰ��ʵ�����С���̬���µĹ��̣���������Ӱ������˼������ͽ������ķ�ʽ�������Ǹ��õض�����ѧ��������ᷢչ����Ҫ�ԡ�
��ѧ��ģ�ĵ����10
������ѧ�ڣ���ѧϰ����ѧ��ģ���ſΣ��Ҿ������������ƵIJ�ͬ������ʵ��ϵ���У��������������ǰ���ǰѧ�õ��Ŀ������ѧ֪ʶӦ�õ�ʵ��������ȥ���ý�ģ��˼�롢���������ʵ�����⣬�����棬����Ҳ�Ӵ���һЩ�����������ʹ�������ܿ�ͳ��˴𰸡�
������ѧϰ�Ĺ����У��һ���˺ܶ�֪ʶ�������зdz������ߡ�ͬʱ������һЩ�������ᡣ
����������ѧϰ��ѧ�Ĺ����о��������ܶ����ѣ��о��ܿ������ѧ��������������ܵȵȣ������ҵ�ѧϰ�����������ͽ����ˣ����Ҳ�֪��ѧ��Ҫ��ô�ã���֪����ʵ���������ﵽ��ͨ��ѧϰ����ѧģ���еĺö�ģ�ͺ��ҷ�����ѧӦ�õĹ㷺�ԡ���ѧģ����һ��ģ�⣬ʹ����ѧ���š���ѧʽ�ӡ�����ͼ�εȶ�ʵ�ʿ��Ȿ�����Եij�����ּ��Ŀ̻��������ܽ���Ĭд��������Ԥ��δ���ķ�չ���ɣ�����Ϊ����ijһ����ķ�չ�ṩij�������µ����Ų��Ի�Ϻò��ԡ���ѧģ��һ�㲢����ʵ�����ֱ�ӷ��棬���Ľ�����������Ҫ���Ƕ���ʵ��������ϸ�Ĺ۲�ͷ���������Ҫ���������������ø�����ѧ֪ʶ������Ӧ��֪ʶ��ʵ�ʿ����г�����������ѧģ�͵Ĺ��̾ͳ�Ϊ��ѧ��ģ������������ѧ�����ڿƼ�����������������ʵ�����⣬����������ѧ�������γɵĽ���ѧ�ƣ���Ҫ�ĺؼ���һ���ǽ����о��������ѧģ�ͣ������Լ�����⡣��ѧ��ģ�ͼ����������֪ʶ���õ����ÿ�ν���绢������
������ѧ��ģ����һ��Ӧ����ѧ��ѧϰ���ſ�Ҫ������ѧ����ν�ʵ�����⾭����������ת��Ϊ����ѧ���⣬Ȼ�������õ���ѧ����ȥ�������ѧ��ģ��һ����ѧ��˼����������������ѧ��.���Ժͷ�����ͨ���������ܽ��ƿ̻������ʵ�������һ��ǿ��������ѧ�ֶΡ���ѧϰ�У���֪������ѧ��ģ�Ĺ��̣���������£�
������1��ģ�������˽������ʵ�ʱ�������ȷ��ʵ�����壬���ն���ĸ�����Ϣ������ѧ�������������⡣
������2��ģ�ͼ��裺����ʵ�ʶ���������ͽ�ģ��Ŀ�ģ���������б�Ҫ�ļ����þ�ȷ���������һЩǡ���ļ��衣
������3��ģ�ͽ������ڼ���Ļ����ϣ������ʵ�����ѧ�������̻�������֮�����ѧ��ϵ��������Ӧ����ѧ�ṹ��
������4��ģ����⣺���û�ȡ�õ��������ϣ���ģ�͵����в����������㡣
������5��ģ�ͷ����������õĽ��������ѧ�ϵķ�����
������6��ģ�ͼ��飺��ģ�ͷ��������ʵ�����ν��бȽϣ��Դ�����֤ģ�͵�ȷ�ԡ������Ժ������ԡ����ģ����ʵ�ʽ��Ǻϣ���Ҫ�Լ�����������ʵ�ʺ��壬�����н��͡����ģ����ʵ���ǺϽϲ��Ӧ���ļ��裬�ٴν��н�ģ���̡�
������ѧģ�ͼ�˳Ӧʱ����չ�ij�����Ҳ���Ͻ����ĸ��Ҫ������ѧ�������ԣ���Ӧ����ѧ������ȷ��ݵļ��㷽�������ܵ���������Ҳ��Ҫ����ѧ������ѧ���߷������ʵ���������ʶ����������ͳ����ѧ��ϵ����������ƫ����ǰ�ߣ���������ѧ��ģ�γ����Ǽ�ǿ���ߵ�һ�ֳ��ԣ���ѧ��ģ�ij�����Ϊ�˰�����������������⣬������������������Ϊѧϰ��ѧģ�͵����������¼��㣺һѧϰ��ѧģ�����ǿ��Բμ���ѧ��ģ����������ѧ��ģ������Ϊ�˴ٽ���ѧ��ģ�ķ�չ��Ӧ�˶����ģ�������������ҵľ�����������ѹ��������������������������ϵ��������������������������д�������������������Ա������������������ȿ�ѧ�ۺ����������ô�ҴӴ�ͳ��֪ʶ����ת�䵽�����������������ǵ�˼���������ʵı仯����Ҳ�������ִ�����ģ�
������ѧϰ��ѧ���������ҵ���˼ά����������ȳ������������ö��˾�����ѧ��ʵ��ң���ɼ��������أ���ѧ��ģ���Ϊ�˽�����������ɱ��ﵣ���Ϊ��ѧ��ģ����Ϊ��������ҵķ�������ͷֽ�������������
������ѧϰ����ѧģ�ͺ������̸����ǵIJ�����һЩ��ѧ����ģ�����˵һЩ��ѧ����������ѧϰ��ģ��ͬʱ�����ø��ֽ�ģ������������DZز����ٵ�matlab��lingo���ȶ��Ƿdz�����ġ���ѧģ������ѧѧϰ���µķ�ʽ����Ϊ�����ṩ������ѧϰ�Ŀռ䣬����������������ѧ�ڽ��ʵ�������еļ�ֵ�����ã�������ѧ���ճ�����������ѧ�Ƶ���ϵ�������ۺ�����֪ʶ�ͷ������ʵ������Ĺ��̣���ǿӦ����ʶ��
����������ѧģ�ͻ����������ۺ���������������������ߡ�������������ȫ�桢��Ƕȿ��������������ʹ���ǵ��������������������������õ��ܺõض�������ߡ���������Ϊ��ѧģ�ʹ����ҵ��Ƿ�ɢ��˼ά�������о��������ֶΡ��̻��ҷ���Ҫ���Լ��Ĵ��£��Լ�������˼ά�����ܾ��������ס���֮ѧϰ��ѧģ�������ڼ������ǵ�ѧϰ��ѧ����Ȥ���ḻ����ѧϰ��ѧ̽����������飻
���������������Ծ����顢������ѧ�ĵ���ѧ֪ʶ�������������ǵ����ĺ���־����
��ѧ��ģ�ĵ����11
������ѧ��ģ�ǵ��������Խ��Խ�����ӵ�һ��ѧ�ƣ�ͨ����ѧ�������ʵ�����⣬��������ѧ������˼ά������������ʵ������������Ҫ�����á����Ҳ�����ѧ��ģ�Ĺ����У�����̵���ᵽ����ѧ��ģ������Ҫ���õ���ѧ����������Ҫ��֡�Ŭ���ͺ����ľ����Լ���ʵ������������ԺͶ���˼����������
�������ȣ���ѧ��ģ��Ҫ���õ���ѧ�������ڽ��ʵ�������'�����У���Ҫ���õ�������ѧ������ģ�ͣ������ͳ�ơ����Թ滮���ַ��̵ȡ�����Щ��Ҫ�����Ǿ߱���ʵ����ѧ��������ˣ��ڲ�����ѧ��ģ֮ǰ������Ҫ��ǿ����ѧ����֪ʶ��ѧϰ��ͬʱҪע����ѧ��ʵ��Ӧ�ã�������ѧ˼ά�ͽ��ʵ�������������
������Σ���ѧ��ģ��Ҫ��֡�Ŭ���ͺ����ľ�����ѧ��ģ����һ�����͵Ĺ��̣���Ҫ���ĺ�����ȥ�����������ѡ���ʵ�ʲ����У����������������ռ���ȫ��ģ������ȷ�����⣬��ʱ������Ҫ���ֻ����ֹ۵���̬�����ϳ��ԺĽ���ͬʱ�����ŶӺ����У�����Ҫ���������������ͬŬ�����γ����ƻ����ĺ�����ϵ�������������һ���������ѧģ�͡�
�������⣬��ѧ��ģ��Ҫ��ʵ������������ԺͶ���˼�����������ڽ��ʵ������ʱ������Ҫ�����Ȿ��������Ĵ������ܹ��������ⱳ��ı��ʺ��ɡ�ͬʱ������ҲҪ�߱�����˼�����������������������˵�����;��飬����Ҫ���Լ��ĽǶ�ȥ�����ͽ�����⡣ֻ��������������ѧ��ģ��ȡ����������Ľ����
���������ѧ��ģ��һ������ѧϰ����ߵĹ��̡���ÿһ��ʵ���У����Ƕ����Դ��м�ȡ���飬�˽��ͬ����ͬ������ص��Ҫ�㡣ͬʱ������ҲҪ��עǰ�ص���ѧ��ģ�ɹ��ͷ�������ʱ�����Լ���֪ʶ�ͼ��ܡ�ͨ������ѧϰ����ߣ����Dz�������ѧ��ģ�ĵ�·��Խ��ԽԶ��ȡ�ø���ɫ�ijɾ͡�
������֮����ѧ��ģ��һ����Ҫ���Ǹ���Ŭ�����ǻ۵�ѧ�ơ�ͨ�����Լ��ľ���������̵���ʶ����ѧ��ģ��������һ��ѧϰ����������һ�ֶ����Լ����ʵ�����������Ļ��ᡣ�ڽ���ѧϰ��ʵ���У��ҽ�����Ŭ������ǿ�Լ�����ѧ������������֡�Ŭ���ͺ����ľ�����߶�ʵ������������ԺͶ���˼��������������ѧϰ����ߣ��Ը��õ�Ӧ����ѧ��ģ����������ս��
��ѧ��ģ�ĵ����12
����һ���µļ�ѵ������˵������������־���棬������֪ʶ�����÷��棬����һ���ѵõĶ������ᡣͨ����ģ�ͣ��������Լ���֪ʶ�棬Ҳ���������֪ʶ���ʵ�����������;ͨ��ģ�����ۣ����Լ������͵�����ͬѧϯλ�Ķ����Ժʹ����Ե�ͬʱ���������Լ����ص��벻�㣬�Ӷ����Լ���`�������˸���̵��˽⡣ͨ����ģ��ѵ�����¼�����Ҹ������
����һ)��Ա֮������������Ҫ��ÿ���˶����س��벻�㣬��Ա֮��Ӧ���������ƻ����������Ա֮��Ҫѧ�ṵͨ���˽�˴˵��ص㡣�ڴ˻����ϣ���Ҫѧ����ϡ�Ҫ�˴���Ϻã��Ҿ��ö�Ա�����������Լ������Ҫ�����������̣������ڶ��ѵ�����Լ����ֲ���ͬʱ����ӦӰ����ѵĻ�����;ÿ����Ա��Ӧ�����Ŷ����θк������У���Ա֮����ɻ�ľ��Ǵ��������ԣ�����������ûˮ�ȡ�����һ���ܺõľ�ʾ;ÿ����Ա��Ҫ�д�ֹۡ���ģ���̶�Ա֮��������������һ�µ�ʱ����ʱ��Ҫ���Ա�����������ǵ�ͷ�ԡ�����Ϊ�ǣ���������������Ķ�Ա�Ҿ��ò��ʺϽ�ģ�����Ƕ�ԱҲ����ʧȥ�Լ���������һζä�ӡ�
������)ÿ����Ա����̬Ҳ�dz���Ҫ�����ȣ�һ����Ҫ�г�ֵ����ģ����dzɹ�������֮һ������Ļ�������һ������Ѿͻ��ӱ�;���⣬һ���˲�Ҫ����������̫�ء��������̫�صĻ���ֻ����������������Ҳ���ʹ�Լ�ȥ��һЩ�������������飬�Ӷ�Ӱ���Լ��ķ��ӡ��Ҹ�����Ϊ���ɹ���һ���Ļ����ɷ֣�һЩ������ǿ�õġ�������ƽʱ�����ԡ���ѧ�㶫����Ϊ�����ġ�
������)����˼ά���������ݺ��ӡ����������������п��Կ�������Щ�д����˼�빹�������ĵ�����㣬����Щ������ǻز����ٵġ���ʵ������˼ά��һ��ϰ�ߡ�ֻҪ���ɴ�ϰ�ߣ�ƽʱ�Ϳ���һ��һ�εĻ��۴�����У����˸��õ�ʱ����Щ��о��п����õ��ϡ�����˵�������ֻ�����ڲ���������֮�ڡ�
��ѧ��ģ�ĵ����13
������ѧ�ڣ���ѧϰ����ѧ��ģ���ſΣ��Ҿ������������ƵIJ�ͬ������ʵ��ϵ���У��������������ǰ���ǰѧ�õ��Ŀ������ѧ֪ʶӦ�õ�ʵ��������ȥ���ý�ģ��˼�롢���������ʵ�����⣬�����棬����Ҳ�Ӵ���һЩ�����������ʹ�������ܿ�ͳ��˴𰸡�
������ѧϰ�Ĺ����У��һ���˺ܶ�֪ʶ�������зdz������ߡ�ͬʱ������һЩ�������ᡣ
����������ѧϰ��ѧ�Ĺ����о��������ܶ����ѣ��о��ܿ������ѧ��������������ܵȵȣ������ҵ�ѧϰ�����������ͽ����ˣ����Ҳ�֪��ѧ��Ҫ��ô�ã���֪����ʵ���������ﵽ��ͨ��ѧϰ����ѧģ���еĺö�ģ�ͺ��ҷ�����ѧӦ�õĹ㷺�ԡ���ѧģ����һ��ģ�⣬ʹ����ѧ���š���ѧʽ�ӡ�����ͼ�εȶ�ʵ�ʿ��Ȿ�����Եij�����ּ��Ŀ̻��������ܽ���Ĭд��������Ԥ��δ���ķ�չ���ɣ�����Ϊ����ijһ����ķ�չ�ṩij�������µ����Ų��Ի�Ϻò��ԡ���ѧģ��һ�㲢����ʵ�����ֱ�ӷ��棬���Ľ�����������Ҫ���Ƕ���ʵ��������ϸ�Ĺ۲�ͷ���������Ҫ���������������ø�����ѧ֪ʶ������Ӧ��֪ʶ��ʵ�ʿ����г�����������ѧģ�͵Ĺ��̾ͳ�Ϊ��ѧ��ģ������������ѧ�����ڿƼ�����������������ʵ�����⣬��
������������ѧ�������γɵĽ���ѧ�ƣ���Ҫ�ĺؼ���һ���ǽ����о��������ѧģ�ͣ������Լ�����⡣��ѧ��ģ�ͼ����������֪ʶ���õ����ÿ�ν���绢������
������ѧ��ģ����һ��Ӧ����ѧ��ѧϰ���ſ�Ҫ������ѧ����ν�ʵ�����⾭����������ת��Ϊ����ѧ���⣬Ȼ�������õ���ѧ����ȥ�������ѧ��ģ��һ����ѧ��˼����������������ѧ�����Ժͷ�����ͨ���������ܽ��ƿ̻������ʵ�������һ��ǿ��������ѧ�ֶΡ���ѧϰ�У���֪������ѧ��ģ�Ĺ��̣���������£�
������1��ģ�������˽������ʵ�ʱ�������ȷ��ʵ�����壬���ն���ĸ�����Ϣ������ѧ�������������⡣
������2��ģ�ͼ��裺����ʵ�ʶ���������ͽ�ģ��Ŀ�ģ���������б�Ҫ�ļ����þ�ȷ���������һЩǡ���ļ��衣
������3��ģ�ͽ������ڼ���Ļ����ϣ������ʵ�����ѧ�������̻�������֮�����ѧ��ϵ��������Ӧ����ѧ�ṹ��
������4��ģ����⣺���û�ȡ�õ��������ϣ���ģ�͵����в����������㡣
������5��ģ�ͷ����������õĽ��������ѧ�ϵķ�����
������6��ģ�ͼ��飺��ģ�ͷ��������ʵ�����ν��бȽϣ��Դ�����֤ģ�͵�ȷ�ԡ������Ժ������ԡ����ģ����ʵ�ʽ��Ǻϣ���Ҫ�Լ�����������ʵ�ʺ��壬�����н��͡����ģ����ʵ���ǺϽϲ��Ӧ���ļ��裬�ٴν��н�ģ���̡�
������ѧģ�ͼ�˳Ӧʱ����չ�ij�����Ҳ���Ͻ����ĸ��Ҫ������ѧ�������ԣ���Ӧ����ѧ������ȷ��ݵļ��㷽�������ܵ���������Ҳ��Ҫ����ѧ������ѧ���߷������ʵ���������ʶ����������ͳ����ѧ��ѧ��ϵ����������ƫ����ǰ�ߣ���������ѧ��ģ�γ����Ǽ�ǿ���ߵ�һ�ֳ��ԣ���ѧ��ģ�ij�����Ϊ�˰�����������������⣬������������������Ϊѧϰ��ѧģ�͵����������¼��㣺һѧϰ��ѧģ�����ǿ��Բμ���ѧ��ģ����������ѧ��ģ������Ϊ�˴ٽ���ѧ��ģ�ķ�չ��Ӧ�˶����ģ�������������ҵľ�����������ѹ��������������������������ϵ��������������������������д�������������������Ա������������������ȿ�ѧ�ۺ����������ô�ҴӴ�ͳ��֪ʶ����ת�䵽������'�����������ǵ�˼���������ʵı仯����Ҳ�������ִ���������ģ���ѧϰ��ѧ���������ҵ���˼ά����������ȳ������������ö��˾�����ѧ��ʵ��ң���ɼ��������أ���ѧ��ģ���Ϊ�˽�����������ɱ��ﵣ���Ϊ��ѧ��ģ����Ϊ��������ҵķ�������ͷֽ�������������
������ѧϰ����ѧģ�ͺ������̸����ǵIJ�����һЩ��ѧ�����֪ʶ������˵һЩ��ѧ����������ѧϰ��ģ��ͬʱ�����ø��ֽ�ģ������������DZز����ٵ�Matlab��Lingo���ȶ��Ƿdz�����ġ���ѧģ������ѧѧϰ���µķ�ʽ����Ϊ�����ṩ������ѧϰ�Ŀռ䣬����������������ѧ�ڽ��ʵ�������еļ�ֵ�����ã�������ѧ���ճ�����������ѧ�Ƶ���ϵ�������ۺ�����֪ʶ�ͷ�
���������ʵ������Ĺ��̣���ǿӦ����ʶ��������ѧģ�ͻ����������ۺ���������������������ߡ�������������ȫ�桢��Ƕȿ��������������ʹ���ǵ��������������������������õ��ܺõض�������ߡ���������Ϊ��ѧģ�ʹ����ҵ��Ƿ�ɢ��˼ά�������о��������ֶΡ��̻��ҷ���Ҫ���Լ��Ĵ��£��Լ�������˼ά�����ܾ��������ס���֮ѧϰ��ѧģ�������ڼ������ǵ�ѧϰ��ѧ����Ȥ���ḻ����ѧϰ��ѧ̽����������飻�����������Ծ����顢������ѧ�ĵ���ѧ֪ʶ�������������ǵ����ĺ���־����
��ѧ��ģ�ĵ����14
�����Ҳμ���һ����Ϊ��Ů���������Ļ���������dz��оٰ��һ����Ҫ������ǣ����ڴ����ܴӽ�����ѧ��һЩ����Ů���ɳ����������Ҫ֪ʶ����ν���������dz������ˣ���Ϊ������������������Ů��ϢϢ��صĻ��⣬���������š����ꡢ�����ȡ�����ν����У��������dz��
�����ڶ��Σ��������š�
�����ڽ����У��ݽ��߽������������ŵ���Ҫ�ԣ��������ǽ����������Լ��������ġ�����������Ҫ�����Լ�����Ҫ���ױ������۹����ҡ�ֻ��ӵ�����ţ����Dz��ܳ�ַ����Լ���DZ�������������Ƿ�����һЩ�������ŵķ�������ѧ�������˽����������Լ�������������ȡ�����ʶ����ֻ�е����Ƕ��Լ�������ʱ�����ܸ��õ�������Ѻʹ��ۡ�
���������Σ����ꡣ
�������������������в��ɻ�ȱ��һ���֣��ݽ����ڽ����и�������ϸ�������������˽������õ����ꡣ����������Ҫ��ϴ��ˣ����ر��˵ĸ��ܡ�����������һЩ��ͨ���ɣ�������������Ͱ��ݡ��Ҵ�������ֻ�����Ĵ��ˣ����Dz��ܻ�����������ꡣ���⣬�����ᵽ�˽����ͻ�ķ������������Ǵ���������֮��ķ����������
�������ĶΣ�������
�������彡�������ǵijɳ���ѧϰ������Ҫ���ݽ�������ν�����Ϊ�����ṩ��һЩ�����Ľ��顣��ǿ���˳����˯�ߡ���������ʳ�Լ��ʵ����˶�����Ҫ�ԡ���������˵������Ҫ�����Լ������壬�������õ�����ϰ�ߡ����⣬�����������ҪԶ�벻��ϰ�ߣ������̡���Ƶȡ���������ᵽ��ֻ��ӵ�н��������ǣ����Dz��ܸ��õ�Ͷ�뵽ѧϰ��������ȥ��
��������Σ��ܽᡣ
����ͨ�����Ů���������Ҷ��������š�����ͽ������˸����ε����⡣����ʶ������Ϊһ��Ů����������Ҫ�������ţ��ᶨ�Լ���`��ֵ�ۣ������˽������õ����꣬��ʱ�̹�ע�Լ������彡�����ⳡ���������������ҵ���Ұ��Ҳ�������Ҷ�δ�����ڴ��������ţ�ֻҪ�����ڳɳ��ĵ�·��Ŭ��ǰ�У�����Ů�����ܳ�Ϊ���š��а��ġ��������ˡ�
��ѧ��ģ�ĵ����15
������һ�Σ����ԣ�120�֣���
������ѧ��ģ��һ��ּ��ͨ����ѧ֪ʶ�����ʵ�������ѧ�ơ���Ϊ�����������ڳ��н�ͨ��ѧϰ��ѧ��ģ�γ̣�����ᵽ����ѧ��ģ�İ������Ȥ������������У��Ҳ���ѧ���˷ḻ����ѧ֪ʶ���������˽������ʹ���˼ά�������������鵽����ѧ�������еľ��ֵ��
�����ڶ��Σ���ʵ����ѧ������240�֣���
������ѧ��ģ��Ϊһ��Ӧ���Ժ�ǿ��ѧ�ƣ�Ҫ�������ڽ��ʵ��������������������ѧ����ѧ֪ʶ���ڳ�����ѧ�γ��У�����ͨ��ѧϰ��ѧ�Ļ�����������ͷ�������������ʵ����ѧ��������Щ֪ʶΪ������ȷ�����Ӧ����ѧ��ģ�ṩ�˼�ʵ�Ļ��������磬��ѧϰ�����Ĺ����У����ǿ���ͨ���������̵���⣬���ʵ�������е�δ֪�������ڼ���ѧ�У����ǿ������ü���ͼ�ε��������Ƶ�������Ľ����������Щ��ѧ֪ʶ������ѧ��ģ�Ļ�ʯ��
���������Σ����Ӧ����ѧ֪ʶ��240�֣���
������ѧϰ��ѧ��ģ�У�����ʶ�����Ӧ����ѧ֪ʶ�ǽ��ʵ������Ĺؼ�����ѧ��ģ�����Ǽ����ù�ʽ�Ͷ���������Ҫ����������ص����������ѧ֪ʶ����⡣���磬�ڽ��ģ���е���������ʱ�����ǿ���ͨ�������ҵ�ʵ�����Ž���������ڽ������ģ���еĹ�������ʱ�����ǿ������ú�����ϵ���������������Ӱ�졣��Щ���Ӧ����ѧ֪ʶ��������ʹ�����ܹ���ʵ���������ҵ����ʵ���ѧ�������ҵ���ѵĽ��������
�������ĶΣ��������ʹ���˼ά��240�֣���
������ѧ��ģ�γ̵�ѧϰ�����У��ҷ��ֽ������ʹ���˼ά�Ƿdz���Ҫ����������ÿ��ģ�͵Ľ������������У����Ƕ���Ҫ����������ȥ˼�����⣬�����ʵ����������ۺϷ��������������Ҫ����ӵ����˼ά��ϵͳ�����ʹ���˼ά�ȶ�����������ѧ��ģ�Ĺ����У����ǿ������ò�ͬ�ķ�����˼άģʽ���ҵ���ѵĽ��������ͨ�����ʵ�����⣬�����������Լ���˼�������ʹ��¾���
��������Σ���ѧ�ľ��ֵ��360�֣���
����ѧ����ѧ��ģ������̸��ܵ�����ѧ�ľ��ֵ����ѧ��ģ�����ܰ������ǽ��ʵ�����⣬�����������ǵ��ۺ����ʺʹ�����������ѧ��ģ�Ĺ�����Ҫ���Ƕ���˼��������̽�ֺͺ�������ʱ��ȡ���Щ���������ʣ���������ѧ��ģ�з�������Ҫ���ã��������ճ������ѧϰ��Ҳ�ܷ��Ӿ��`���������⣬��ѧ��ģ���������������ǵĿ�ѧ�����ѧϰ̬�ȣ������Ǹ����Ȱ���ѧ�Ϳ�ѧ����ѧ��ģ�ǽ��������ѧ֪ʶת��Ϊʵ��Ӧ�õĹ��̣�ʹ���Ǹ��õ���������ѧ��ʵ��Ӧ�ú����塣
�����ܽᣨ120�֣���
����ͨ��ѧϰ��ѧ��ģ�γ̣��Ҳ�����������ʵ����ѧ֪ʶ���������˽��ʵ������ʹ���˼ά����������ѧ��ģ������ᵽ����ѧ�ľ��ֵ��ʵ��Ӧ�á�����ҽ�����Ŭ��ѧϰ��ѧ��ģ֪ʶ������Ϊ��Ӧ�Կ��ԣ�����Ϊ�������Լ����ۺ����ʺʹ���������Ϊδ����ѧϰ�ͷ�չ���¼�ʵ�Ļ�����
����ѧ��ģ�ĵ���������£�
��ѧ��ģ��ѵ�ĵ����07-29
��ѧ��ģЭ���ܽ�05-29
��ҵ����е��ģ��ְ��06-11
��ѧ�ĵ����05-21
��ѧ�ĵ����02-14
��ѧ��ѧ�ĵ����06-20
��ѧ��ѧ���ĵ����01-16
��ѧ��ѵ�ĵ����01-06
��ѧ�����ĵ����02-04